Saturday, 18 May 2019
Monday, 13 May 2019
Algebra of Predicates versus K.Yu. Polyakov, Sets and Logic in the Unified State Examination Problems // Informatics , № 10, 2015
Consider three complicated cases for every clone of classical problem #18 of USE in Informatics ( Russian abbreviation EGE )
1. Solution of challenging equation with mixed basic predicates of type E() && DEL() via technique proposed by Helen Mironchick
2. Solution of the equation E(M)⊕E(N) => E(A)*¬E(M & N) ≡ 1 via the calculus of basic predicates according to Helen Mironchick
3. Predicate algebra and classical examples of the Unified State Examination in Informatics problem #18
Segments of the real axis and discrete sets of integers
*********
Case 1
*********
Solution of challenging equation with mixed basic predicates of type E() && DEL() via technique proposed by Helen Mironchick
1. Solution of challenging equation with mixed basic predicates of type E() && DEL() via technique proposed by Helen Mironchick
2. Solution of the equation E(M)⊕E(N) => E(A)*¬E(M & N) ≡ 1 via the calculus of basic predicates according to Helen Mironchick
3. Predicate algebra and classical examples of the Unified State Examination in Informatics problem #18
Segments of the real axis and discrete sets of integers
*********
Case 1
*********
Solution of challenging equation with mixed basic predicates of type E() && DEL() via technique proposed by Helen Mironchick
Denote by DEL (n, m) the statement "a natural number n is divided without a remainder by a positive integer m". For what is the smallest natural number A, the formula
(D(34)⊕D(51) => ¬D(A)^D(272)) v Е(15) ≡ 1
is identically true (that is, it takes the value 1 for any natural value of the variable x)?
The absorption of predicates of type ¬D() from one basis in a disjunction and the suppression of predicates of type D() from one basis in a conjunction makes the calculus constructed by Helen Mironchik a universal approach that converts problem 18's DEL() of any complexity into a simple equation in DEL() predicates.
Further notice belongs to Helen :-
D(16) = ¬E(1)*¬E(2)*¬E(4)*¬E(8) =
= ¬(E(1) v E(2) v E(4) v E(8)) = ¬E(15)
E(15)=¬D(16)
Convert original equation from implication to disjunction
(D(34)≡D(51)) v ¬D(A)^D(272)) v ¬D(16) ≡ 1
D(34)^D(51) v ¬D(34)^¬D(51) v ¬D(A)^D(272)) v ¬D(16) ≡ 1
D(34)^D(51) v ¬D(34)^¬D(51) v ¬D(A)^D(17)^D(16) v ¬D(16) ≡ 1
Suppress D(17) in first and fourth terms via ¬D(17),
then suppress D(2^4) via ¬D(2^4) in fourth term
D(34) = D(2)^D(17)
D(51) = D(3)^D(17)
D(31)^D(51) = D(2)^D(3)^D(17)
¬D(34) = (¬D(2) v ¬D(17))
¬D(51) = (¬D(3) v ¬D(17))
¬D(34)^¬D(51) = ¬D(2)^¬D(3) v ¬D(17)
D(2)^D(3)^D(17) v ¬D(2)^¬D(3) v ¬D(17) v
v ¬D(A)^D(17)^D(2^4) v ¬D(2^4) ≡ 1
D(6) v ¬D(2)^¬D(3) v ¬D(17) v ¬D(A) v ¬D(2^4) ≡ 1
Thus A(min) = 6
*********
Case 2
*********
Solution of the equation E(M)⊕E(N) => E(A)*¬E(M & N) ≡ 1 via the calculus of basic predicates according to Helen Mironchick
In general we follow guidelines of technique developed in
http://kpolyakov.spb.ru/download/mea18bit.pdf
Per link mentioned above (quoting Helen A. Mironchick)
Let Et (x) be a predicate whose truth set is all x for which x & t ≠ 0.
If t is a power of two, then such a predicate will be called basic.
The basic predicate describes (fixes) a single unit in the binary notation.
Further, for brevity, the predicate Et (x) will be denoted by E(t);
we will also denote the truth set of this predicate.
(quoting ends)
Once again the decomposition of E() type predicates into logical sum of basic predicates , which are actually predicates associated with powers of 2. The decomposition itself works as universal approach for solving the problems #18 of per bits conjunction type having any level of complexity. Here is important to understand the principal difference between Bitwise2 technique and technique relying on decomposition into basic predicates. The last one
provide quite straight forward way to suppress the factors of ¬E(2^s) type in conjuction via terms of E(2^s) type coming into equation to be logically added to conjunction kind of ¬E(2^5)*¬E(2^4)*¬E(2^3)*¬E(2^1) + E(2^5) + E(2^3) + E(2^1) = ¬E(2^4) + E(2^5) + E(2^3) + E(2^1)
Denote by {X} the binary representation of a natural number X.
The core statement of the post below is :-
Let R, M, N be natural numbers. R is the minimum
satisfying the condition {M OR N} = {R OR {M & N}},
where "OR" is a bitwise disjunction, and "&" is a bitwise conjunction
Then the smallest A satisfying the equation
E(M)⊕E(N)=>E(A)*¬E (M & N) ≡ 1 would be equal R.
First we intend to show that, E(M) v E(N) = E(R) v E(M&N).
Notice also that everywhere below "*" is "^".
Consider expansions in the logical sum of basic predicates.
E (M) and E(N). All pairs of equal basic predicates will be
collapsed into one and the logical sum of such predicate pairs
will obviously give E(M&N). The logical sum of all those
remaining is exactly E(R). It remains to apply the formulas
of De Morgan.
¬(E(M) v E(N)) = ¬(E(R) v E(M & N))
and get the required equality below
¬E(M)*¬E(N) = ¬E(R)*¬E(M&N) (1)
Bitwise2 has a familiar formula. Due to the fact that ¬E(N) = Z(N)
Z(M)*Z(N) = Z(M OR N) = Z(R)*Z(M & N)
Thus, ¬E(M)*¬E(N) = ¬E(R)*¬E (M & N) can be obtained
as a result of Statement 3 of http://kpolyakov.spb.ru/download/bitwise2.pdf
Convert the original equation as follows
E(M)⊕E(N) => E(A)*¬E(M&N) ≡ 1
(E(M)≡E(N)) v E(A)*¬E(M&N) ≡ 1
¬E(M)*¬E(N) v E(M)*E(N) v E(A)*¬E(M&N) ≡ 1
From the decomposition of M and N into basic predicates
define the numbers REST-M and REST-N such that
each of them has no common unit bits with M&N and in doing so
obtain
{REST-M} + {M & N} = {M}
{REST-N} + {M & N} = {N}
Consequently
E(M) = E(REST-M) v E(M&N)
E(N) = E(REST-N) v E(M&N)
Apply formula (1) to ¬E(M)*¬E(N):-
¬E(R)*¬E(M&N) v (E(REST-M) v E(M & N))*(E(REST-N) v E(M&N)) v
v E(A)*¬E(M&N) ≡ 1
¬E(R)*¬E(M&N) v E(REST-M)*E(REST-N) v E (M&N) v
v E(A)*¬E(M&N) ≡ 1
¬E(R) v E(REST-M)*E(REST-N) v E(M&N) v E(A)≡ 1
*******************
Theorem 1
*******************
For truth ∀ x: E(k)(x) => E(m)(x), it is necessary
and sufficient that the set of unit bits "k" is fully
included in the set of unit bits "m"
Necessity
Let j(1), .., j(s) be the numbers of the single unit bits "k",
ordered descending (for example), then
¬E(k)= ¬E(j(1)) * .... *¬E(j(s)) we show that
¬E(k) + E(m) = 1
We have
¬E(k) = ¬E(j(1))* .... *¬E(j(s))
E(m) = E(j(1)) + ... + E(j(s)) + E (rest)
We consistently suppress all factors in conjunction.
¬E(k) + E (m) = ¬E(j(1))* ....*¬E(j(s)) + E(j(1)) + ... + E(j(s)) + E(rest) = 1
Sufficiency
If there is at least one single unit bit "k" (with the number "p") not included
in the single unit bits "m", then k&2^p! = 0 and at the same time the numbers
of the single unit bits "m" do not contain "p", then 2^p with a unit at the place "p" in the binary representation 1000 ... 0 (counting from 0 from right to left)
will be multiplied by 0 in the p-th position "m", that is, m&2^p = 0
In this case, k&2^p != 0, that is, E(k,2^p) = 1 if
m&2^p = 0 then E(m,2^p) = 0
In this case, Е(к,2^p) => Е(m,2^p) = 0, that is,
the condition of the theorem is not satisfied for all "x"
We are all set with Theorem 1
Starting from this point we intend to invoke Theorem 1 where it
appears to be needed without any previous notification
Say $(X) is the set of unit bits in X.
Convert the last equation as follows
(E(R)=> E(REST-M))*(E(R)=> E(REST-N))
v (E(R)=> E(M&N)) v (E(R)=> E(A)) ≡ 1
Assign A(min) value equal R and consider any A < A(min) then
∃ j: ( j !∈ $(A))^(j ∈ $(R)) = True
From here and below our major goal is to prove that for any
A < A(min) it exists integer y=y(A) which will result
(E(R)=> E(REST-M))*(E(R)=> E(REST-N))
v (E(R)=> E(M&N)) v (E(R)=> E(A)) (y(A)) =0
Set unit bit on place number "j" in y=y(A)
Due to j ∈ $(R) this j !∈ $(M&N). The rest of y's bits
let us set to 0
Notice that this "j" also doesn't belong to at least one of sets
$(REST-M) or $(REST-N), otherwise it would belong
$(M&N). So conjuction below is equal 0.
(E(R,y)=> E(REST-M,y))*(E(R,y)=> E(REST-N,y)) = 0 (1)
Then notice that (E(R,y)=> E(M&N,y)) = 0 (2)
and (E(R,y)=> E(A,y) = 0 (3)
Finally we are getting (due to (1),(2) and (3))
(E(R)=> E(REST-M))*(E(R)=> E(REST-N)) v
v (E(R)=> E(M&N)) v (E(R)=> E(A))(y) = 0
Thus for any A less then R it exists y=y(A) such
that predicate been written above has value 0
for number y=y(A) and A(min) appears to be real
minimum A(min)
*********
Case 3
*********
Predicate algebra and classical examples of the Unified State Examination problem Informatics № 18 ( Segments of the real axis and discrete sets of integers )
See
1) Алгебра предикатов и классические примеры задач ЕГЭ Информатика № 18
2) See Алгебра предикатов и классические задачи ЕГЭ Информатика № 18 с XOR и "~"
Refences
1. A. Mironchik, ALGEBRA OF PREDICATES AND RELATED GEOMETRIC MODELS CREATION IN REGARDS OF UNIFIED STATE EXAMINATION IN INFORMATICS (RUSSIAN EGE) ,
Informatics at school №3 , 2019
2. http://kpolyakov.spb.ru/download/mea18bit.pdf
Subscribe to:
Comments (Atom)
Featured Post
Solution of one USE Informatics system of Boolean equations in 08.2016 style
Original system Orinal system ¬(x1≡x2)v¬(x1≡x3)^(x2≡x3)=1 ¬(x3≡x4)v¬(x3≡x5)^(x4≡x5)=1 ¬(x5≡x6)v¬(x5≡x7)^(x6≡x7)=1 ¬(x7≡x8)v¬(x7≡x9...
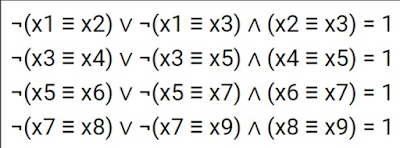
-
((x1=x2)+x3)+x4+!x5=1 ((x2=x3)+x4)+x5+!x6=1 ((x3=x4)+x5)+x6+!x7=1 ((x4=x5)+x6)+x7+!x8=1 Опускание на один уровень ниже должно,в при...
-
https://vk.com/informatics_100?z=photo-40390768_457277148%2Fwall-40390768_199869 Fork two 08.2016 charts Notice that ¬X1=>...





