Original source
Intentionally consider more complicated system
(((x1∧y1)) ≡ (x2∧y2)) => (x3∧y3))=1
(((x2∧y2)) ∨ ¬(x3∧y3)) => (x4∧y4))=1
(((x3∧y3)) ≡ (x4∧y4)) => (x5∧y5))=1
(((x4∧y4)) ∨ ¬(x5∧y5)) => (x6∧y6))=1
Introduce predicate z(x,y)= (x^y).
Power of false set is equal 3.
Power of truth set is equal 1.
Would you replace z(x,y) with w(x,y)=(xVy).
Power of false set is equal 1.
Power of truth set is equal 3.
The general approach will stay the same - outgoing
numbers and initial values would be updated correspondingly,
but arrows charts would stay the same
Denote zj=xj^xj
Convert system into zj variables
(1)
(z1≡z2) => z3 =1
(z2∨¬z3) => z4 =1
(z3≡z4) => z5=1
(z4∨¬z5) => z6 =1
(2)
(z1≡z2) => z3 =1
(z3 => z2) => z4 =1
(z3≡z4) => z5=1
(z5 => z4) => z6 =1
Consider system
(((x1Vy1)) ≡ (x2Vy2)) => (x3Vy3))=1
(((x2Vy2)) ∨ ¬(x3Vy3)) => (x4Vy4))=1
(((x3Vy3)) ≡ (x4Vy4)) => (x5Vy5))=1
(((x4Vy4)) ∨ ¬(x5Vy5)) => (x6Vy6))=1
Denote wj=(xjVyj) . Notice that arrows charts are exactly the same.
Initial values and outgoing numbers has been updated due to different powers
of truth and false sets of predicate w(x,y)=(xVy), 3 and 1 correspondingly
(w1≡w2) => w3 =1
(w3 => w2) => w4 =1
(w3≡w4) => w5=1
(w5 => w4) => w6 =1
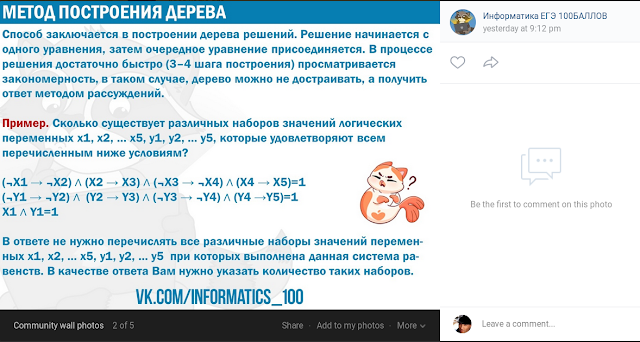

 Consider system
Consider system 



