Original task
Solution
System below is equivalent to original one.
The previous system is supposed to make convertion itself
a real headaches generator
(x1=>x2)^(y2=>y1)^(x1 v y1)=1
(x2=>x3)^(y3=>y2)^(x2 v y2)=1
(x3=>x4)^(y4=>y3)^(x3 v y3)=1
(x4=>x5)^(y5=>y4)^(x4 v y4)=1
(x5=>x6)^(y6=>y5)^(x5 v y5)=1
x6 v y6=1
Proceed with building fork diagram with transition pair (x2,y2) && forking matrix
Passing Polyakov's Control
Solution
System below is equivalent to original one.
The previous system is supposed to make convertion itself
a real headaches generator
(x1=>x2)^(y2=>y1)^(x1 v y1)=1
(x2=>x3)^(y3=>y2)^(x2 v y2)=1
(x3=>x4)^(y4=>y3)^(x3 v y3)=1
(x4=>x5)^(y5=>y4)^(x4 v y4)=1
(x5=>x6)^(y6=>y5)^(x5 v y5)=1
x6 v y6=1
Proceed with building fork diagram with transition pair (x2,y2) && forking matrix
Passing Polyakov's Control



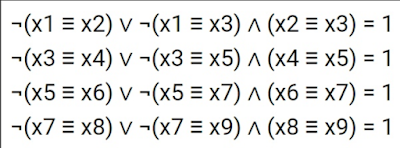


No comments:
Post a Comment