B.D.
Down here we rely on technique proposed in
https://mapping-metod.blogspot.com/2019/03/blog-post.html
Original system
((x1^x2=>x3)^x4=>x5)^x6=>x7=1
((y1^y2=>y3)^y4=>y5)^y6=>y7=1
x1=>y7=1
#1 - x1
#2 - x1^x2
#3 - (x1^x2=>x3)
#4 - (x1^x2=>x3)^x4
#5 - (x1^x2=>x3)^x4=>x5)
#6 - (x1^x2=>x3)^x4=>x5)^x6
#7 - ((x1^x2=>x3)^x4=>x5)^x6=>x7=1
Passing Polyakov's Control
Another system solved via pass to center per Helen Mironchick unpublished manuscript
((x1^x2=>x3)^x4=>x5)^x6=>x7=1
((y1^y2=>y3)^y4=>y5)^y6=>y7=1
x1=>y5=1
#1 - x1
#2 - x1^x2
#3 - (x1^x2=>x3)
#4 - (x1^x2=>x3)^x4
#5 - (x1^x2=>x3)^x4=>x5)
#6 - (x1^x2=>x3)^x4=>x5)^x6
#7 - ((x1^x2=>x3)^x4=>x5)^x6=>x7=1
Passing Polyakov's Control




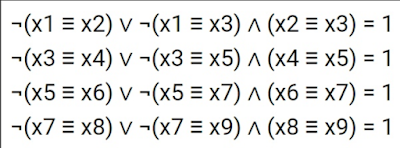


No comments:
Post a Comment