Original system
(((x1=>x2)=>x3)=>x4)=>x5=1
(((y1=>y2=>y3)=>y4)=>y5=1
(((z1=>z2)=>z3)=>z4)=>z5=1
(x3=>y3)^(y4=>z4)=1
Solution below is based on Helen Mironchick article in meantime pending publication. Intellectual property for idea of "Reverse pass to center" completely belongs Helen Mironchick. We just place in play her technique awaiting publication.
For X-LINE
#2 is (x1=>x2)
#3 is (x1=>x2)=>x3
#4 is ((x1=>x2)=>x3)=x4
#5 is (((x1=>x2)=>x3)=x4)=>x5
For Y-LINE and Z-LINE replace x by y and x by z correspondingly
*******************
Chaining order
*******************
1) We get x3 via reverse pass to center
2) Getting y3 via simple implication
3) Getting y4 via reverse pass to center
Here we have y1=>y2=>y3 (#3) Y-LINE.
Perform move from #5 to #4 in the opposite direction.
Now calculate y4 as usual.
4) Getting z4 via simple implication
5) Completing Z-LINE having z4 (on line-0 213,on line-1-333)
Second system:-
Each one of system's equations are built upon sample 9 from
http://kpolyakov.spb.ru/download/mea-2013-10.pdf for x,y and z.
Variables x4,y5,z6 specifically selected to revert different diagrams from mentioned article.
See page 23, which contains original straight forward diagrams.

Testing for z6 numbers {64,39}

Third system :-
(x1=>x2)^(x2=>x3)^(x3=>x4)^(x4=>x5)^(x5=>x6)=1
(y1=>y2)^(y2=>y3)^(y3=>y4)^(y4=>y5)^(y5=>y6)=1
(z1=>z2)^(z2=>z3)^(z3=>z4)^(z4=> z5)^(z5=> z6)=1
x3^y4^z5=0

(((x1=>x2)=>x3)=>x4)=>x5=1
(((y1=>y2=>y3)=>y4)=>y5=1
(((z1=>z2)=>z3)=>z4)=>z5=1
(x3=>y3)^(y4=>z4)=1
Solution below is based on Helen Mironchick article in meantime pending publication. Intellectual property for idea of "Reverse pass to center" completely belongs Helen Mironchick. We just place in play her technique awaiting publication.
For X-LINE
#2 is (x1=>x2)
#3 is (x1=>x2)=>x3
#4 is ((x1=>x2)=>x3)=x4
#5 is (((x1=>x2)=>x3)=x4)=>x5
For Y-LINE and Z-LINE replace x by y and x by z correspondingly
*******************
Chaining order
*******************
1) We get x3 via reverse pass to center
2) Getting y3 via simple implication
3) Getting y4 via reverse pass to center
Here we have y1=>y2=>y3 (#3) Y-LINE.
Perform move from #5 to #4 in the opposite direction.
Now calculate y4 as usual.
4) Getting z4 via simple implication
5) Completing Z-LINE having z4 (on line-0 213,on line-1-333)
Second system:-
Each one of system's equations are built upon sample 9 from
http://kpolyakov.spb.ru/download/mea-2013-10.pdf for x,y and z.
Variables x4,y5,z6 specifically selected to revert different diagrams from mentioned article.
See page 23, which contains original straight forward diagrams.
((x1^x2=>x3)^x4=>x5)^x6=>x7 = 1
((y1^y2=>y3)^y4=>y5)^y6=>y7 = 1
((z1^z2=>z3)^z4=>z5)^z6 =>z7 = 1
(x4=>y5)=>z6=1

Testing for z6 numbers {64,39}

Third system :-
(x1=>x2)^(x2=>x3)^(x3=>x4)^(x4=>x5)^(x5=>x6)=1
(y1=>y2)^(y2=>y3)^(y3=>y4)^(y4=>y5)^(y5=>y6)=1
(z1=>z2)^(z2=>z3)^(z3=>z4)^(z4=> z5)^(z5=> z6)=1
x3^y4^z5=0



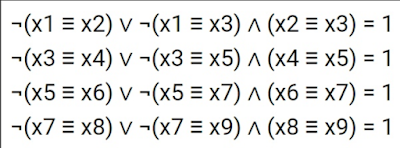


No comments:
Post a Comment