This is a kind of joke, of course, and yet your main misconception is that the mapping method is currently not what they say in the videos on the Internet for USE Informatics problem 23. The mapping method in meantime is how Helen Mironchick solves the 23rd problem in each particular case. Obviously the sentence been pronounced is my very personal opinion and you might ignore it completely.
Original systems. Each one of system's equations are built upon sample 9 from
http://kpolyakov.spb.ru/download/mea-2013-10.pdf for x,y and z.
Variables x4,y5,z6 specifically selected to revert different diagrams from mentioned article.
See page 23, which contains original straight forward diagrams.
Consider two following systems
(1)
((x1^x2=>x3)^x4=>x5)^x6=>x7 = 1
((y1^y2=>y3)^y4=>y5)^y6=>y7 = 1
((z1^z2=>z3)^z4=>z5)^z6=>z7 = 1
(x4=>y5)=>z6=1
(2)
((x1^x2=>x3)^x4=>x5)^x6=>x7 = 1
((y1^y2=>y3)^y4=>y5)^y6=>y7 = 1
((z1^z2=>z3)^z4=>z5)^z6 =>z7 = 1
(x4^y5)=>z6=1
Solution below is based on Helen Mironchick article in meantime pending publication. Intellectual property for idea of "Reverse pass to center" completely belongs Helen Мironchick. Solution down here extensively using "reverse pass to center"
Control performed via Polyakov's Calculator
Testing for z6 numbers {64,39}
Final test crashes on Polyakov's Calculator
Consider a bit different system
((x1^x2=>x3)^x4=>x5)^x6=>x7 = 1
((y1^y2=>y3)^y4=>y5)^y6=>y7 = 1
((z1^z2=>z3)^z4=>z5)^z6 =>z7 = 1
(x4^y5)=>z6=1
Obviously values obtained via "Reverse pass to center" stays the same. Thus we recalculate only the last Boolean expression:-
Original systems. Each one of system's equations are built upon sample 9 from
http://kpolyakov.spb.ru/download/mea-2013-10.pdf for x,y and z.
Variables x4,y5,z6 specifically selected to revert different diagrams from mentioned article.
See page 23, which contains original straight forward diagrams.
Consider two following systems
(1)
((x1^x2=>x3)^x4=>x5)^x6=>x7 = 1
((y1^y2=>y3)^y4=>y5)^y6=>y7 = 1
((z1^z2=>z3)^z4=>z5)^z6=>z7 = 1
(x4=>y5)=>z6=1
(2)
((x1^x2=>x3)^x4=>x5)^x6=>x7 = 1
((y1^y2=>y3)^y4=>y5)^y6=>y7 = 1
((z1^z2=>z3)^z4=>z5)^z6 =>z7 = 1
(x4^y5)=>z6=1
Solution below is based on Helen Mironchick article in meantime pending publication. Intellectual property for idea of "Reverse pass to center" completely belongs Helen Мironchick. Solution down here extensively using "reverse pass to center"
Final test crashes on Polyakov's Calculator
Consider a bit different system
((x1^x2=>x3)^x4=>x5)^x6=>x7 = 1
((y1^y2=>y3)^y4=>y5)^y6=>y7 = 1
((z1^z2=>z3)^z4=>z5)^z6 =>z7 = 1
(x4^y5)=>z6=1
Obviously values obtained via "Reverse pass to center" stays the same. Thus we recalculate only the last Boolean expression:-
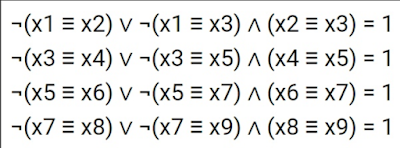
No comments:
Post a Comment