Original problem
On right hand side of equations we put 1 instead 0 to avoid
building quite simple Mapping Method arrows diagrams.
The intend is to build more complicated ones
(x1^y1≡x2^y2) =>x3^y3=1
(x3^y3=>x2^y2) =>x4^y4=1
(x3^y3≡x4^y4) =>x5^y5=1
(x5^y5=>x4^y4) =>x6^y6=1
Introduce double predicates zj=(xj)^(yj) . The power of zj truth set is 1 .
Just one pair of bits {1,1}, the power of zj false set is 3 .
False set contains three pairs of bits {1,0; 0,1; 0,0}.
In general utilizing of predicates for solving 23rd problem is described here
https://mapping-metod.blogspot.com/2019/07/blog-post.html
System itself
(z1≡z2) =>z3 =1
(z3=>z2) =>z4 =1
(z3≡z4)=>z5 =1
(z5=>z4) =>z6 =1
Notice that outgoing numbers should match powers of truth and false sets
of predicate zj
Advantages of predicates approach when solving 23rd problem.
Consider a bit more complicated system kind of
(x1^y1^z1≡x2^y2^z2) =>x3^y3^z3=1
(x3^y3^z3=>x2^y2^z2) =>x4^y4^z4=1
(x3^y3^z3≡x4^y4^z4) =>x5^y5^z5=1
(x5^y5^z5=>x4^y4^z5) =>x6^y6^z6=1
Introduce triple predicates zj=(xj)^(yj)^(zj) . The power of zj truth set is 1 .
Just one triple of bits {1,1,1}, the power of zj false set is 7 .
Regarding predicates zj system keeps to stay the same
(z1≡z2) =>z3 =1
(z3=>z2) =>z4 =1
(z3≡z4)=>z5 =1
(z5=>z4) =>z6 =1
Notice that outgoing numbers should match powers of truth and false sets
of predicate zj
On right hand side of equations we put 1 instead 0 to avoid
building quite simple Mapping Method arrows diagrams.
The intend is to build more complicated ones
(x1^y1≡x2^y2) =>x3^y3=1
(x3^y3=>x2^y2) =>x4^y4=1
(x3^y3≡x4^y4) =>x5^y5=1
(x5^y5=>x4^y4) =>x6^y6=1
Introduce double predicates zj=(xj)^(yj) . The power of zj truth set is 1 .
Just one pair of bits {1,1}, the power of zj false set is 3 .
False set contains three pairs of bits {1,0; 0,1; 0,0}.
In general utilizing of predicates for solving 23rd problem is described here
https://mapping-metod.blogspot.com/2019/07/blog-post.html
System itself
(z1≡z2) =>z3 =1
(z3=>z2) =>z4 =1
(z3≡z4)=>z5 =1
(z5=>z4) =>z6 =1
Notice that outgoing numbers should match powers of truth and false sets
of predicate zj
Advantages of predicates approach when solving 23rd problem.
Consider a bit more complicated system kind of
(x1^y1^z1≡x2^y2^z2) =>x3^y3^z3=1
(x3^y3^z3=>x2^y2^z2) =>x4^y4^z4=1
(x3^y3^z3≡x4^y4^z4) =>x5^y5^z5=1
(x5^y5^z5=>x4^y4^z5) =>x6^y6^z6=1
Introduce triple predicates zj=(xj)^(yj)^(zj) . The power of zj truth set is 1 .
Just one triple of bits {1,1,1}, the power of zj false set is 7 .
Regarding predicates zj system keeps to stay the same
(z1≡z2) =>z3 =1
(z3=>z2) =>z4 =1
(z3≡z4)=>z5 =1
(z5=>z4) =>z6 =1
Notice that outgoing numbers should match powers of truth and false sets
of predicate zj



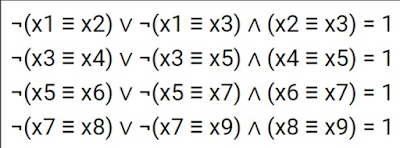


No comments:
Post a Comment