See also:-
Setting up a cross-reference table in 08/2016 approach of Helen Mironchick when moving to a new line of the system of Boolean equations
in this post another case with triple predicates and much more complicated 08/2016 chart is considered.
Consider system of Boolean equations.
(1) F1(x1,y1)≡F2(x2,y2) =1
(2) F1(x2,y2)≡F2(x3,y3) =1Setting up a cross-reference table in 08/2016 approach of Helen Mironchick when moving to a new line of the system of Boolean equations
in this post another case with triple predicates and much more complicated 08/2016 chart is considered.
Consider system of Boolean equations.
(1) F1(x1,y1)≡F2(x2,y2) =1
. . . . . .
(7) F1(x7,y7)≡F2(x8,y8) =1
where F1 and F2 are double predicates
Denote card(N) the power of set N
Denote n1,n2,m1,m2,s1,s2
n1=card (falseSet_F2 ∩ falseSet_F1)
n2=card (falseSet_F2 ∩ truthSet_F1)
m1=card (truthSet_F2 ∩ falseSet_F1)
m2=card (truthSet_F2 ∩ truthSet_F1)
s1=card (falseSet_F1)
s2=card (truthSet_F1)
Then following 08.2016 diagram takes place
For instance consider system
(1) F1(x1,y1)=>F2(x2,y2) =1
(2) F1(x2,y2)=>F2(x3,y3) =1
. . . . . .
(7) F1(x7,y7)=>F2(x8,y8) =1
where F1 and F2 are double predicates
Then following 08.2016 diagram would take place
Another sample
(1) F1(x1,y1) v F2(x2,y2) =1
(2) F1(x2,y2) v F2(x3,y3) =1
. . . . . .
(7) F1(x7,y7) v F2(x8,y8) =1
where F1 and F2 are double predicates
Would I consider triple predicates instead of double it wouldn't change excel spreadsheets.
Core logic proposed in the very first rows keeps stay the same.
Now consider system from inform20190916proba2.pdf

Fork 08.2016 diagram




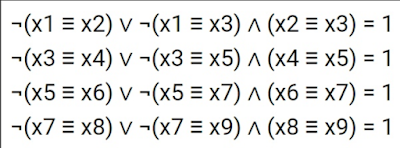


No comments:
Post a Comment