Optimal approach to solve Russian Unified State Examination (USE) 18,23 problems
Friday, 13 December 2019
Tuesday, 29 October 2019
The 23 -rd USE's Informatics task casual support on VK Informatics_100 on the go (UPDATE 1)
https://vk.com/informatics_100?z=photo-40390768_457277148%2Fwall-40390768_199869
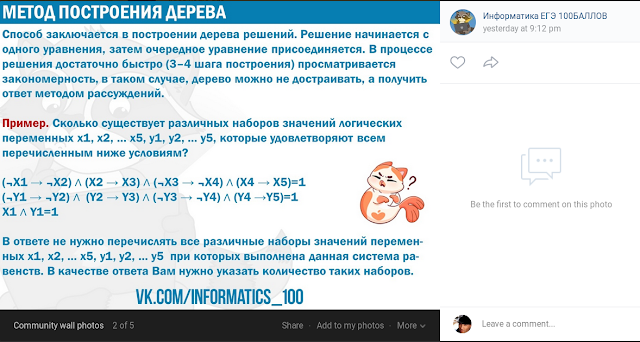
Fork two 08.2016 charts
Notice that ¬X1=>¬X2≡X2=>X1 and ¬X3=>¬X4≡X4=>X3
Thursday, 24 October 2019
Style 08.2016 on the go (Solving systems of Boolen Equations for USE Informatics)
Original system
(x1=>y1)^(x1 v x2)^¬(x1^x2)=1
(x2=>y2)^(x2 v x3)^¬(x2^x3)=1
(x3=>y3)^(x3 v x4)^¬(x3^x4)=1
(x4=>y4)^(x4 v x5)^¬(x4^x5)=1
(x5=>y5)^(x5 v x6)^¬(x5^x6)=1
(x6=>y6)^(x6 v x7)^¬(x6^x7)=1
(x7=>y7)=1
Notice first ( due to De Morgan rules ) :-
(x1 v x2)^¬(x1^x2)=(x1 v x2)^(¬x1 v ¬x2)=
=x1^¬x2 v x2^¬x1 = x1⊕x2
Convert to equivalent
(x1=>y1)^(x1⊕x2)=1
(x2=>y2)^(x2⊕x3)=1
(x3=>y3)^(x3⊕x4)=1
(x4=>y4)^(x4⊕x5)=1
(x5=>y5)^(x5⊕x6)=1
(x6=>y6)^(x6⊕x7)=1
(x7=>y7)=1
Fork 08.2016 chart to solve the system
(x1=>y1)^(x1 v x2)^¬(x1^x2)=1
(x2=>y2)^(x2 v x3)^¬(x2^x3)=1
(x3=>y3)^(x3 v x4)^¬(x3^x4)=1
(x4=>y4)^(x4 v x5)^¬(x4^x5)=1
(x5=>y5)^(x5 v x6)^¬(x5^x6)=1
(x6=>y6)^(x6 v x7)^¬(x6^x7)=1
(x7=>y7)=1
Notice first ( due to De Morgan rules ) :-
(x1 v x2)^¬(x1^x2)=(x1 v x2)^(¬x1 v ¬x2)=
=x1^¬x2 v x2^¬x1 = x1⊕x2
Convert to equivalent
(x1=>y1)^(x1⊕x2)=1
(x2=>y2)^(x2⊕x3)=1
(x3=>y3)^(x3⊕x4)=1
(x4=>y4)^(x4⊕x5)=1
(x5=>y5)^(x5⊕x6)=1
(x6=>y6)^(x6⊕x7)=1
(x7=>y7)=1
Fork 08.2016 chart to solve the system
Monday, 21 October 2019
Solution of one USE Informatics system of Boolean equations in 08.2016 style
Original system
Orinal system
¬(x1≡x2)v¬(x1≡x3)^(x2≡x3)=1
¬(x3≡x4)v¬(x3≡x5)^(x4≡x5)=1
¬(x5≡x6)v¬(x5≡x7)^(x6≡x7)=1
¬(x7≡x8)v¬(x7≡x9)^(x8≡x9)=1
Convert to equivalent
(x1≡x2) => (x1⊕x3)^(x2≡x3) =1
(x3≡x4) => (x3⊕x5)^(x4≡x5) =1
(x5≡x6) => (x5⊕x7)^(x6≡x7) =1
(x7≡x8) => (x7⊕x9)^(x8≡x9) =1
Here we have transition variables x3,x5,x7 rather then transition pairs
between equations. Thus we would manage via 08.2016 charts.
Consider a bit more complex sample of similar system
((x1≡x2)≡x3)=>(x1⊕x4)^((x2≡x3)≡x4)=1
((x4≡x5)≡x6)=>(x4⊕x7)^((x5≡x6)≡x7)=1
((x7≡x8)≡x9)=>(x7⊕x10)^((x8≡x9)≡x10)=1
Transition variables are x4 and x7. Fork 08.2016 chart for this system
Orinal system
¬(x1≡x2)v¬(x1≡x3)^(x2≡x3)=1
¬(x3≡x4)v¬(x3≡x5)^(x4≡x5)=1
¬(x5≡x6)v¬(x5≡x7)^(x6≡x7)=1
¬(x7≡x8)v¬(x7≡x9)^(x8≡x9)=1
Convert to equivalent
(x1≡x2) => (x1⊕x3)^(x2≡x3) =1
(x3≡x4) => (x3⊕x5)^(x4≡x5) =1
(x5≡x6) => (x5⊕x7)^(x6≡x7) =1
(x7≡x8) => (x7⊕x9)^(x8≡x9) =1
Here we have transition variables x3,x5,x7 rather then transition pairs
between equations. Thus we would manage via 08.2016 charts.
Consider a bit more complex sample of similar system
((x1≡x2)≡x3)=>(x1⊕x4)^((x2≡x3)≡x4)=1
((x4≡x5)≡x6)=>(x4⊕x7)^((x5≡x6)≡x7)=1
((x7≡x8)≡x9)=>(x7⊕x10)^((x8≡x9)≡x10)=1
Transition variables are x4 and x7. Fork 08.2016 chart for this system
The solution of one well-known problem from the USE Informatics forum in the format 08.2016 (Russian Federation)
Original wording in Helen Mironchikc's group
https://vk.com/club180658320?w=wall-180658320_64%2Fall
The first pass looks for the total number of solutions of the system, the second pass considers the number of false decisions. Answer: 448 - 32 = 416
https://vk.com/club180658320?w=wall-180658320_64%2Fall
The first pass looks for the total number of solutions of the system, the second pass considers the number of false decisions. Answer: 448 - 32 = 416
Saturday, 19 October 2019
Разбор СтатГрад 23.09.2019 Информатика ЕГЭ №23 vs решение в стиле 08.2016 той же задачи 23
Оригинальное решение
https://www.youtube.com/watch?time_continue=4&v=_Hf22YG3uU0
Разобрали по СтатГраду ответ 81 ( титанические усилия завершаются с ошибкой - "1" по строке "01" должна быть удалена так как y8=>x8=1 )
Решение в стиле 08.2016 ( с правильным ответом при этом еще и предоставляет foolproof by default )
(x1=>x2)^(y2=>y1)=1
(x2=>x3)^(y3=>y2)=1
(x3=>x4)^(y4=>y3)=1
(x4=>x5)^(y5=>y4)=1
(x5=>x6)^(y6=>y5)=1
(x6=>x7)^(y7=>y6)=1
(x7=>x8)^(y8=>y7)=1
(y8=>x8)=1
https://www.youtube.com/watch?time_continue=4&v=_Hf22YG3uU0
Разобрали по СтатГраду ответ 81 ( титанические усилия завершаются с ошибкой - "1" по строке "01" должна быть удалена так как y8=>x8=1 )
Решение в стиле 08.2016 ( с правильным ответом при этом еще и предоставляет foolproof by default )
(x1=>x2)^(y2=>y1)=1
(x2=>x3)^(y3=>y2)=1
(x3=>x4)^(y4=>y3)=1
(x4=>x5)^(y5=>y4)=1
(x5=>x6)^(y6=>y5)=1
(x6=>x7)^(y7=>y6)=1
(x7=>x8)^(y8=>y7)=1
(y8=>x8)=1
Thursday, 17 October 2019
Algebra of predicates {D(k)} (Helen Mironchick ) versus Advanced Implication usage by Natalya Konina regarding problem 132 from ege18.doc
Original task
Solution bellow differs from the original one proposed by Helen Mironchick
to address question of Anastasia Stepanenko, however it is still based on algebra of {D(k)} ( see [1] ) .
Solution itself
D(A) v ¬D(24)^¬D(36) ≡1
D(24)≡ D(2^3)^D(3)
D(36)≡ D(3^2)^D(2^2)
¬D(24)^¬D(36)≡(¬D(2^3) v ¬D(3))^(¬D(3^2) v ¬D(2^2))≡
¬D(2^3)^¬D(3^2) v ¬D(2^3)^¬D(2^2) v ¬D(3)^¬D(3^2) v ¬D(3)^¬D(2^2)
Due to
¬D(3)^¬D(3^2)≡ ¬D(3)
¬D(2^3)^¬D(2^2)≡ ¬D(2^2)
Getting
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3) v ¬D(3)^¬D(2^2)≡ ¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)
because ¬D(3) absorbs ¬D(3)^¬D(2^2)
Per De Morgan rules
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)≡ ¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))
¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))≡ ¬(D(8) v D(9)) v ¬D(12)
Finally we obtain
D(А) v ¬(D(8) v D(9)) v ¬D(12) ≡1
Hence A(min)=12
You might want to compare it with solution provided in
http://kpolyakov.spb.ru/download/ege18del.pdf
for the task 132
References
1. E.A. Mironchick ALGEBRA OF PREDICATES AND RELATED GEOMETRIC MODELS CREATION IN REGARDS OF UNIFIED STATE EXAM IN INFORMATICS (RUSSIAN EGE) , Informatics in school #3 2019
Solution bellow differs from the original one proposed by Helen Mironchick
to address question of Anastasia Stepanenko, however it is still based on algebra of {D(k)} ( see [1] ) .
Solution itself
D(A) v ¬D(24)^¬D(36) ≡1
D(24)≡ D(2^3)^D(3)
D(36)≡ D(3^2)^D(2^2)
¬D(24)^¬D(36)≡(¬D(2^3) v ¬D(3))^(¬D(3^2) v ¬D(2^2))≡
¬D(2^3)^¬D(3^2) v ¬D(2^3)^¬D(2^2) v ¬D(3)^¬D(3^2) v ¬D(3)^¬D(2^2)
Due to
¬D(3)^¬D(3^2)≡ ¬D(3)
¬D(2^3)^¬D(2^2)≡ ¬D(2^2)
Getting
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3) v ¬D(3)^¬D(2^2)≡ ¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)
because ¬D(3) absorbs ¬D(3)^¬D(2^2)
Per De Morgan rules
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)≡ ¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))
¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))≡ ¬(D(8) v D(9)) v ¬D(12)
Finally we obtain
D(А) v ¬(D(8) v D(9)) v ¬D(12) ≡1
Hence A(min)=12
You might want to compare it with solution provided in
http://kpolyakov.spb.ru/download/ege18del.pdf
for the task 132
References
1. E.A. Mironchick ALGEBRA OF PREDICATES AND RELATED GEOMETRIC MODELS CREATION IN REGARDS OF UNIFIED STATE EXAM IN INFORMATICS (RUSSIAN EGE) , Informatics in school #3 2019
Wednesday, 16 October 2019
Решение задачи №132 из ege18.doc в Алгебре Предикатов {D(k)}
Условие
Алгебрa Предикатов {D(k)} определена в [1].
Решение
D(A) v ¬D(24)^¬D(36) ≡1
D(24)≡ D(2^3)^D(3)
D(36)≡ D(3^2)^D(2^2)
¬D(24)^¬D(36)≡(¬D(2^3) v ¬D(3))^(¬D(3^2) v ¬D(2^2))≡
¬D(2^3)^¬D(3^2) v ¬D(2^3)^¬D(2^2) v ¬D(3)^¬D(3^2) v ¬D(3)^¬D(2^2)
Так как
¬D(3)^¬D(3^2)≡ ¬D(3)
¬D(2^3)^¬D(2^2)≡ ¬D(2^2)
Получаем :-
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3) v ¬D(3)^¬D(2^2)≡ ¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)
поскольку ¬D(3) поглощает ¬D(3)^¬D(2^2)
Два последних слагаемых сворачиваем по де Моргану
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)≡ ¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))
¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))≡ ¬(D(8) v D(9)) v ¬D(12)
Окончательно имеем
D(А) v ¬(D(8) v D(9)) v ¬D(12) ≡1
Откуда A(min)=12
Ссылки
1. Елена А. Мирончик АЛГЕБРА ПРЕДИКАТОВ
И ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКИХ МОДЕЛЕЙ
НА ЕГЭ ПО ИНФОРМАТИКЕ , ИВШ №3 2019
Алгебрa Предикатов {D(k)} определена в [1].
Решение
D(A) v ¬D(24)^¬D(36) ≡1
D(24)≡ D(2^3)^D(3)
D(36)≡ D(3^2)^D(2^2)
¬D(24)^¬D(36)≡(¬D(2^3) v ¬D(3))^(¬D(3^2) v ¬D(2^2))≡
¬D(2^3)^¬D(3^2) v ¬D(2^3)^¬D(2^2) v ¬D(3)^¬D(3^2) v ¬D(3)^¬D(2^2)
Так как
¬D(3)^¬D(3^2)≡ ¬D(3)
¬D(2^3)^¬D(2^2)≡ ¬D(2^2)
Получаем :-
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3) v ¬D(3)^¬D(2^2)≡ ¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)
поскольку ¬D(3) поглощает ¬D(3)^¬D(2^2)
Два последних слагаемых сворачиваем по де Моргану
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)≡ ¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))
¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))≡ ¬(D(8) v D(9)) v ¬D(12)
Окончательно имеем
D(А) v ¬(D(8) v D(9)) v ¬D(12) ≡1
Откуда A(min)=12
Ссылки
1. Елена А. Мирончик АЛГЕБРА ПРЕДИКАТОВ
И ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКИХ МОДЕЛЕЙ
НА ЕГЭ ПО ИНФОРМАТИКЕ , ИВШ №3 2019
Monday, 14 October 2019
Решение одной задачи на побитную конъюнкцию в Алгебре Предикатов {E(k)}
Алгебра Предикатов {E(k}} определена в http://kpolyakov.spb.ru/download/mea18bit.pdf
Пусть {N(j)} j=1,2,...,m - конечное множество натуральных чисел.
Найти наименьшее А при котором имеет место следующее тождество
(E(N(1) =>(E(N(2) =>(E(N(3 )=> . . . .=>(E(N(m)) =>E(A)) . . . . ))) ≡1
Решение.
Преобразуем исходное выражение к виду:-
m
v (¬E(N(j) ) v E(A) ≡ 1
j=1
m
¬( ^ E(N(j) ) v E(A) ≡ 1
j=1
m
( ^ E(N(j) ) => E(A) ≡ 1
j=1
Эквивалентно
m
¬E(A) => ¬( ^ E(N(j) ) ≡ 1
j=1
Далее
m
¬E(A) => ( v ¬E(N(j) ) ≡ 1
j=1
В силу дистрибутивности импликации
по отношению к дизъюнкции :-
m
v (¬E(A) => ¬E(N(j) ) ≡ 1
j=1
Эквивалентно
m
v ( E(N(j) => E(A) ) ≡ 1
j=1
По теореме 1 в https://mapping-metod.blogspot.com/2019/02/2017-versus-bitwise2-1-2.html
получаем A(min) = min{N(j)}
j=1,2,..,m
Если нет ни одного N(j) все биты которого входят в А то последняя дизъюнкция не может быть равна тождественно 1 , так как каждое слагаемое дает бит, не входящий в А, строим двоичное число z0 , содержащие все эти биты (наличие совпадающих только упрощает ситуацию)
Тогда
m
( v (E(N(j) => E(A))(z0) = 0
j=1
то есть если А < A(min), то каждое N(j) имеет такой бит и найденное А(min) действительно минимально.
Следствие
Любая задача вида Е(M)=>(E(N)=>E(A)) ≡ 1 тривиальна A=min{M,N}
Например
Пусть {N(j)} j=1,2,...,m - конечное множество натуральных чисел.
Найти наименьшее А при котором имеет место следующее тождество
(E(N(1) =>(E(N(2) =>(E(N(3 )=> . . . .=>(E(N(m)) =>E(A)) . . . . ))) ≡1
Решение.
Преобразуем исходное выражение к виду:-
m
v (¬E(N(j) ) v E(A) ≡ 1
j=1
m
¬( ^ E(N(j) ) v E(A) ≡ 1
j=1
m
( ^ E(N(j) ) => E(A) ≡ 1
j=1
Эквивалентно
m
¬E(A) => ¬( ^ E(N(j) ) ≡ 1
j=1
Далее
m
¬E(A) => ( v ¬E(N(j) ) ≡ 1
j=1
В силу дистрибутивности импликации
по отношению к дизъюнкции :-
m
v (¬E(A) => ¬E(N(j) ) ≡ 1
j=1
Эквивалентно
m
v ( E(N(j) => E(A) ) ≡ 1
j=1
По теореме 1 в https://mapping-metod.blogspot.com/2019/02/2017-versus-bitwise2-1-2.html
получаем A(min) = min{N(j)}
j=1,2,..,m
Если нет ни одного N(j) все биты которого входят в А то последняя дизъюнкция не может быть равна тождественно 1 , так как каждое слагаемое дает бит, не входящий в А, строим двоичное число z0 , содержащие все эти биты (наличие совпадающих только упрощает ситуацию)
Тогда
m
( v (E(N(j) => E(A))(z0) = 0
j=1
то есть если А < A(min), то каждое N(j) имеет такой бит и найденное А(min) действительно минимально.
Следствие
Любая задача вида Е(M)=>(E(N)=>E(A)) ≡ 1 тривиальна A=min{M,N}
Например
Sunday, 13 October 2019
Predicates truth and false sets regarding solving problems 23 USE Informatics VK's News Wire
Original source
Intentionally consider more complicated system
(((x1∧y1)) ≡ (x2∧y2)) => (x3∧y3))=1
(((x2∧y2)) ∨ ¬(x3∧y3)) => (x4∧y4))=1
(((x3∧y3)) ≡ (x4∧y4)) => (x5∧y5))=1
(((x4∧y4)) ∨ ¬(x5∧y5)) => (x6∧y6))=1
Introduce predicate z(x,y)= (x^y).
Power of false set is equal 3.
Power of truth set is equal 1.
Would you replace z(x,y) with w(x,y)=(xVy).
Power of false set is equal 1.
Power of truth set is equal 3.
The general approach will stay the same - outgoing
numbers and initial values would be updated correspondingly,
but arrows charts would stay the same
Denote zj=xj^xj
Convert system into zj variables
(1)
(z1≡z2) => z3 =1
(z2∨¬z3) => z4 =1
(z3≡z4) => z5=1
(z4∨¬z5) => z6 =1
(2)
(z1≡z2) => z3 =1
(z3 => z2) => z4 =1
(z3≡z4) => z5=1
(z5 => z4) => z6 =1
Consider system
(((x1Vy1)) ≡ (x2Vy2)) => (x3Vy3))=1
(((x2Vy2)) ∨ ¬(x3Vy3)) => (x4Vy4))=1
(((x3Vy3)) ≡ (x4Vy4)) => (x5Vy5))=1
(((x4Vy4)) ∨ ¬(x5Vy5)) => (x6Vy6))=1
Denote wj=(xjVyj) . Notice that arrows charts are exactly the same.
Initial values and outgoing numbers has been updated due to different powers
of truth and false sets of predicate w(x,y)=(xVy), 3 and 1 correspondingly
(w1≡w2) => w3 =1
(w3 => w2) => w4 =1
(w3≡w4) => w5=1
(w5 => w4) => w6 =1
Intentionally consider more complicated system
(((x1∧y1)) ≡ (x2∧y2)) => (x3∧y3))=1
(((x2∧y2)) ∨ ¬(x3∧y3)) => (x4∧y4))=1
(((x3∧y3)) ≡ (x4∧y4)) => (x5∧y5))=1
(((x4∧y4)) ∨ ¬(x5∧y5)) => (x6∧y6))=1
Introduce predicate z(x,y)= (x^y).
Power of false set is equal 3.
Power of truth set is equal 1.
Would you replace z(x,y) with w(x,y)=(xVy).
Power of false set is equal 1.
Power of truth set is equal 3.
The general approach will stay the same - outgoing
numbers and initial values would be updated correspondingly,
but arrows charts would stay the same
Denote zj=xj^xj
Convert system into zj variables
(1)
(z1≡z2) => z3 =1
(z2∨¬z3) => z4 =1
(z3≡z4) => z5=1
(z4∨¬z5) => z6 =1
(2)
(z1≡z2) => z3 =1
(z3 => z2) => z4 =1
(z3≡z4) => z5=1
(z5 => z4) => z6 =1
Consider system
(((x1Vy1)) ≡ (x2Vy2)) => (x3Vy3))=1
(((x2Vy2)) ∨ ¬(x3Vy3)) => (x4Vy4))=1
(((x3Vy3)) ≡ (x4Vy4)) => (x5Vy5))=1
(((x4Vy4)) ∨ ¬(x5Vy5)) => (x6Vy6))=1
Denote wj=(xjVyj) . Notice that arrows charts are exactly the same.
Initial values and outgoing numbers has been updated due to different powers
of truth and false sets of predicate w(x,y)=(xVy), 3 and 1 correspondingly
(w1≡w2) => w3 =1
(w3 => w2) => w4 =1
(w3≡w4) => w5=1
(w5 => w4) => w6 =1
Saturday, 12 October 2019
Solution via decomposition into basic predicates several problems 18-th currently posted to Informatics_100 News Wire
Solution via decomposition into basic predicates
E(77)=E(64) v E(8) v E(4) v E(1) ;
E(12)=E(8) v E(4)
Now original equation has been converted per De Morgan rules:-
¬E(77) v E(12) v E(A) ≡ 1;
¬E(64)^¬E(8)^¬E(4)^¬E(1) v E(8) v E(4) v E(A) ≡ 1
Suppress E(8) and E(4) in conjunction
¬E(64)^¬E(1) v E(12) v E(A) ≡ 1 ;
¬E(65) v E(12) v E(A) ≡ 1
Hence A(min) = 65
¬E(33)=>(E(45)=>E(A)) ≡ 1
E(33) v ¬E(45) v E(A) ≡ 1
E(33)=E(32) v E(1) ;
E(45)=E(32) v E(8) v E(4) v E(1)
E(32) v E(1) v ¬E(32)^¬E(8)^¬E(4)^¬E(1) v E(A) ≡ 1
Suppress E(32) and E(1) in conjunction
E(32) v E(1) v ¬E(8)^¬E(4) v E(A) ≡ 1;
E(33) v ¬(E(8) v E(4)) v E(A) ≡ 1
E(33) v ¬E(12) v E(A) ≡ 1
Hence
A(min)=12
Subscribe to:
Comments (Atom)
Featured Post
Solution of one USE Informatics system of Boolean equations in 08.2016 style
Original system Orinal system ¬(x1≡x2)v¬(x1≡x3)^(x2≡x3)=1 ¬(x3≡x4)v¬(x3≡x5)^(x4≡x5)=1 ¬(x5≡x6)v¬(x5≡x7)^(x6≡x7)=1 ¬(x7≡x8)v¬(x7≡x9...

-
((x1=x2)+x3)+x4+!x5=1 ((x2=x3)+x4)+x5+!x6=1 ((x3=x4)+x5)+x6+!x7=1 ((x4=x5)+x6)+x7+!x8=1 Опускание на один уровень ниже должно,в при...
-
Алгебра Предикатов {E(k}} определена в http://kpolyakov.spb.ru/download/mea18bit.pdf Пусть {N(j)} j=1,2,...,m - конечное множество натура...
























