Original task
Solution bellow differs from the original one proposed by Helen Mironchick
to address question of Anastasia Stepanenko, however it is still based on algebra of {D(k)} ( see [1] ) .
Solution itself
D(A) v ¬D(24)^¬D(36) ≡1
D(24)≡ D(2^3)^D(3)
D(36)≡ D(3^2)^D(2^2)
¬D(24)^¬D(36)≡(¬D(2^3) v ¬D(3))^(¬D(3^2) v ¬D(2^2))≡
¬D(2^3)^¬D(3^2) v ¬D(2^3)^¬D(2^2) v ¬D(3)^¬D(3^2) v ¬D(3)^¬D(2^2)
Due to
¬D(3)^¬D(3^2)≡ ¬D(3)
¬D(2^3)^¬D(2^2)≡ ¬D(2^2)
Getting
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3) v ¬D(3)^¬D(2^2)≡ ¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)
because ¬D(3) absorbs ¬D(3)^¬D(2^2)
Per De Morgan rules
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)≡ ¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))
¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))≡ ¬(D(8) v D(9)) v ¬D(12)
Finally we obtain
D(А) v ¬(D(8) v D(9)) v ¬D(12) ≡1
Hence A(min)=12
You might want to compare it with solution provided in
http://kpolyakov.spb.ru/download/ege18del.pdf
for the task 132
References
1. E.A. Mironchick ALGEBRA OF PREDICATES AND RELATED GEOMETRIC MODELS CREATION IN REGARDS OF UNIFIED STATE EXAM IN INFORMATICS (RUSSIAN EGE) , Informatics in school #3 2019
Solution bellow differs from the original one proposed by Helen Mironchick
to address question of Anastasia Stepanenko, however it is still based on algebra of {D(k)} ( see [1] ) .
Solution itself
D(A) v ¬D(24)^¬D(36) ≡1
D(24)≡ D(2^3)^D(3)
D(36)≡ D(3^2)^D(2^2)
¬D(24)^¬D(36)≡(¬D(2^3) v ¬D(3))^(¬D(3^2) v ¬D(2^2))≡
¬D(2^3)^¬D(3^2) v ¬D(2^3)^¬D(2^2) v ¬D(3)^¬D(3^2) v ¬D(3)^¬D(2^2)
Due to
¬D(3)^¬D(3^2)≡ ¬D(3)
¬D(2^3)^¬D(2^2)≡ ¬D(2^2)
Getting
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3) v ¬D(3)^¬D(2^2)≡ ¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)
because ¬D(3) absorbs ¬D(3)^¬D(2^2)
Per De Morgan rules
¬D(2^3)^¬D(3^2) v ¬D(2^2) v ¬D(3)≡ ¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))
¬(D(2^3)vD(3^2) v ¬(D(2^2)^D(3))≡ ¬(D(8) v D(9)) v ¬D(12)
Finally we obtain
D(А) v ¬(D(8) v D(9)) v ¬D(12) ≡1
Hence A(min)=12
You might want to compare it with solution provided in
http://kpolyakov.spb.ru/download/ege18del.pdf
for the task 132
References
1. E.A. Mironchick ALGEBRA OF PREDICATES AND RELATED GEOMETRIC MODELS CREATION IN REGARDS OF UNIFIED STATE EXAM IN INFORMATICS (RUSSIAN EGE) , Informatics in school #3 2019

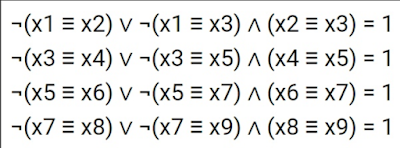


No comments:
Post a Comment