Original system
((x1vy1)^z1 ≡ (x3vy3)^z3)=>((x2vy2)^z2) =1
((x2vy2)^z2)⊕ ((x4vy4)^z4))=>((x3vy3)^z3) =1
((x3vy3)^z3 ≡ (x5vy5)^z5)=>((x4vy4)^z4) =1
((x4vy4)^z4)⊕ ((x6vy6)^z6))=>((x5vy5)^z5) =1
Now make a substitution ( kind of design had been suggested in P-40 from ege23.pdf )
w1=(x1 v y1)^z1


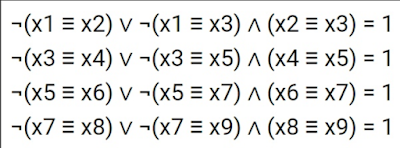


No comments:
Post a Comment