This post was initiated by the analysis of the approach of Helen A. Mironchick to the task P-40 from ege23.doc.
Let F (x, y, z) be a triple predicate defined on the set of all three bit chains. The truth set of this predicate is exactly 5 different chains, specific bits included in the chains of truth do not matter.Consider the system of equations.
F (x1, y1, z1) ≡ F (x3, y3, z3) => F (x2, y2, z2) = 1
F (x2, y2, z2) ⊕ F (x4, y4, z4) => F (x3, y3, z3) = 1
F (x3, y3, z3) ≡ F (x5, y5, z5) => F (x4, y4, z4) = 1
F (x4, y4, z4) ⊕ F (x6, y6, z6) => F (x5, y5, z5) = 1
Setw1 = F (x1, y1, z1)
w2 = F (x2, y2, z2)
w3 = F (x3, y3, z3)
w4 = F (x4, y4, z4)
w5 = F (x5, y5, z5)
w6 = F (x6, y6, z6)
Then we plot the diagrams and generateMapping Method table
Consider three cases. Truth sets of each
of the predicates considered below consists of 5 three bit
chains, its own for each predicate constructed
F (x, y, z) = ((x => y) => z);
F (x, y, z) = (x => y ^ z);
F (x, y, z) = ((x v y) => z);
Calculate according to Polyakov each case (POC - Proof of concept)
Thus, for a system that can be reduced to the traditional matrix of the Mapping Method for w (j) variables, the result is determined only by the power of the truth set of the predicate, and not by the formula defining F (x, y, z)




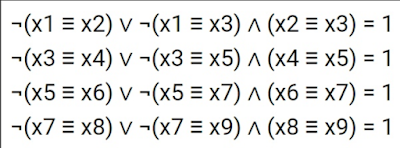


No comments:
Post a Comment