Original
((x1≡y1) =>(x2≡y2)) ^ (x1 v y1)=1
((x2≡y2) =>(x3≡y3)) ^ (x2 v y2)=1
((x3≡y3) =>(x4≡y4)) ^ (x3 v y3)=1
((x4≡y4) =>(x5≡y5)) ^ (x4 v y4)=1
((x5≡y5) =>(x6≡y6)) ^ (x5 v y5)=1
((x6≡y6) =>(x7≡y7)) ^ (x6 v y6)=1
((x7≡y7) =>(x8≡y8)) ^ (x7 v y7)=1
x8 v y8=1
As soon as we have a conditions that allow us to determine the bits of x(j),y(j) for the arrows outgoing from the node of the 08/2016 chart, we can start. In particular case, we are ready to go ahead with 08/2016 diagram style. In other words, we have to know bits combination associated with arrows sequence connecting neighboring nodes in chart .

Control P116 via Polyakov's calculator
((x1≡y1) =>(x2≡y2)) ^ (x1 v y1)=1
((x2≡y2) =>(x3≡y3)) ^ (x2 v y2)=1
((x3≡y3) =>(x4≡y4)) ^ (x3 v y3)=1
((x4≡y4) =>(x5≡y5)) ^ (x4 v y4)=1
((x5≡y5) =>(x6≡y6)) ^ (x5 v y5)=1
((x6≡y6) =>(x7≡y7)) ^ (x6 v y6)=1
((x7≡y7) =>(x8≡y8)) ^ (x7 v y7)=1
x8 v y8=1
As soon as we have a conditions that allow us to determine the bits of x(j),y(j) for the arrows outgoing from the node of the 08/2016 chart, we can start. In particular case, we are ready to go ahead with 08/2016 diagram style. In other words, we have to know bits combination associated with arrows sequence connecting neighboring nodes in chart .
Here you might want to compare solution for P175 proposed by Informatic BU . See
solution of the P175 provided via 08/2016 chart

Control P116 via Polyakov's calculator





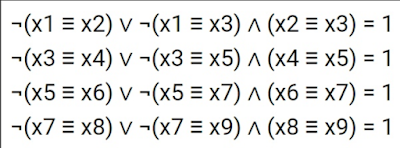


No comments:
Post a Comment