Original system
(x1^y1^z1)⊕(x3^y3^z3) =>((x2=>y2)=>z2)^((x2≡y2)≡z2)=1
(x2^y2^z2)⊕(x4^y4^z4) =>((x3=>y3)=>z3)^((x3≡y3)≡z3)=1
(x3^y3^z3)⊕(x5^y5^z5) =>((x4=>y4)=>z4)^((x4≡y4)≡z4)=1
(x4^y4^z4)⊕(x6^y6^z6) =>((x5=>y5)=>z5)^((x5≡y5)≡z5)=1
Notice that 2 is power of truth_set\{1,1,1} of predicate F(x,y,z)=((x=>y)=>z)^((x≡y)≡z)
Base diagram per Helen Mironchick has been set and Mapping Method table has been
forked as well.
(x1^y1^z1)⊕(x3^y3^z3) =>((x2=>y2)=>z2)^((x2≡y2)≡z2)=1
(x2^y2^z2)⊕(x4^y4^z4) =>((x3=>y3)=>z3)^((x3≡y3)≡z3)=1
(x3^y3^z3)⊕(x5^y5^z5) =>((x4=>y4)=>z4)^((x4≡y4)≡z4)=1
(x4^y4^z4)⊕(x6^y6^z6) =>((x5=>y5)=>z5)^((x5≡y5)≡z5)=1
Notice that 2 is power of truth_set\{1,1,1} of predicate F(x,y,z)=((x=>y)=>z)^((x≡y)≡z)
Base diagram per Helen Mironchick has been set and Mapping Method table has been
forked as well.


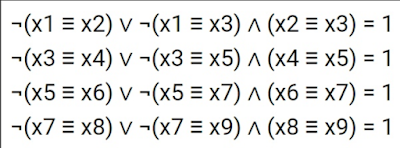


No comments:
Post a Comment